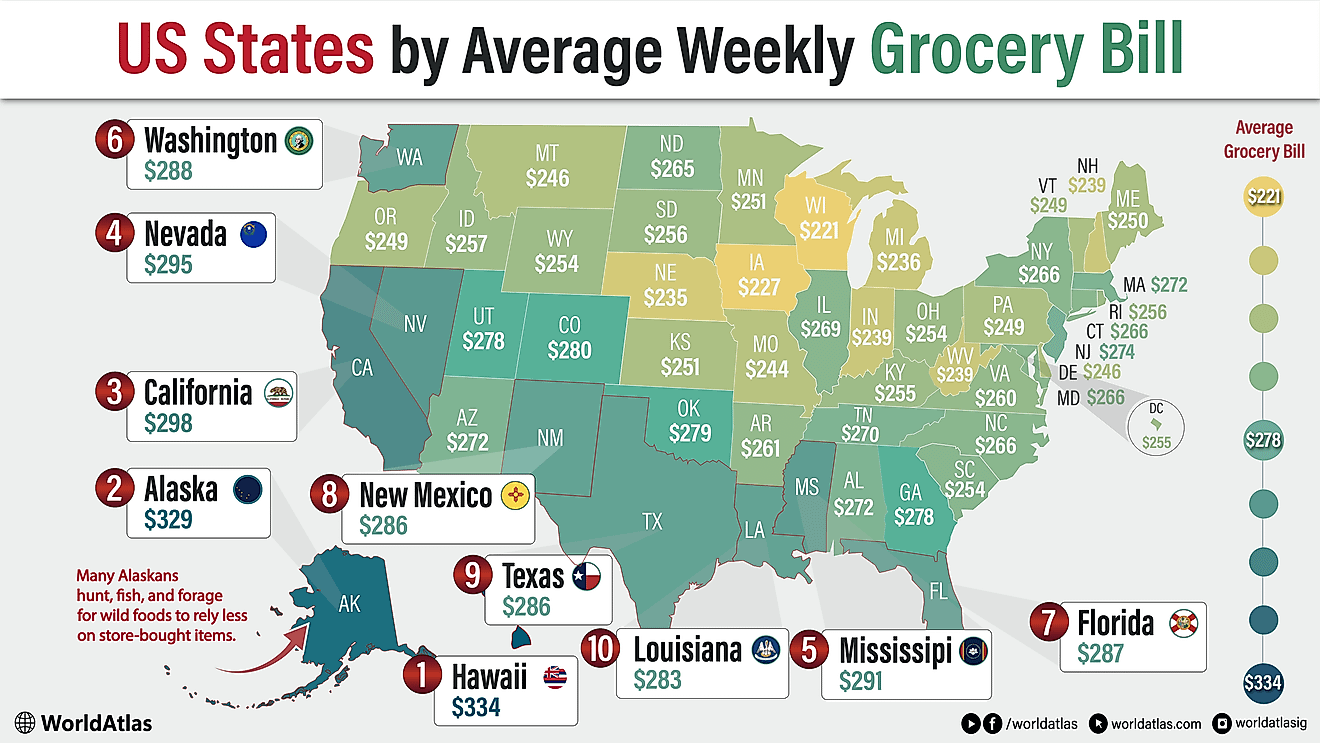
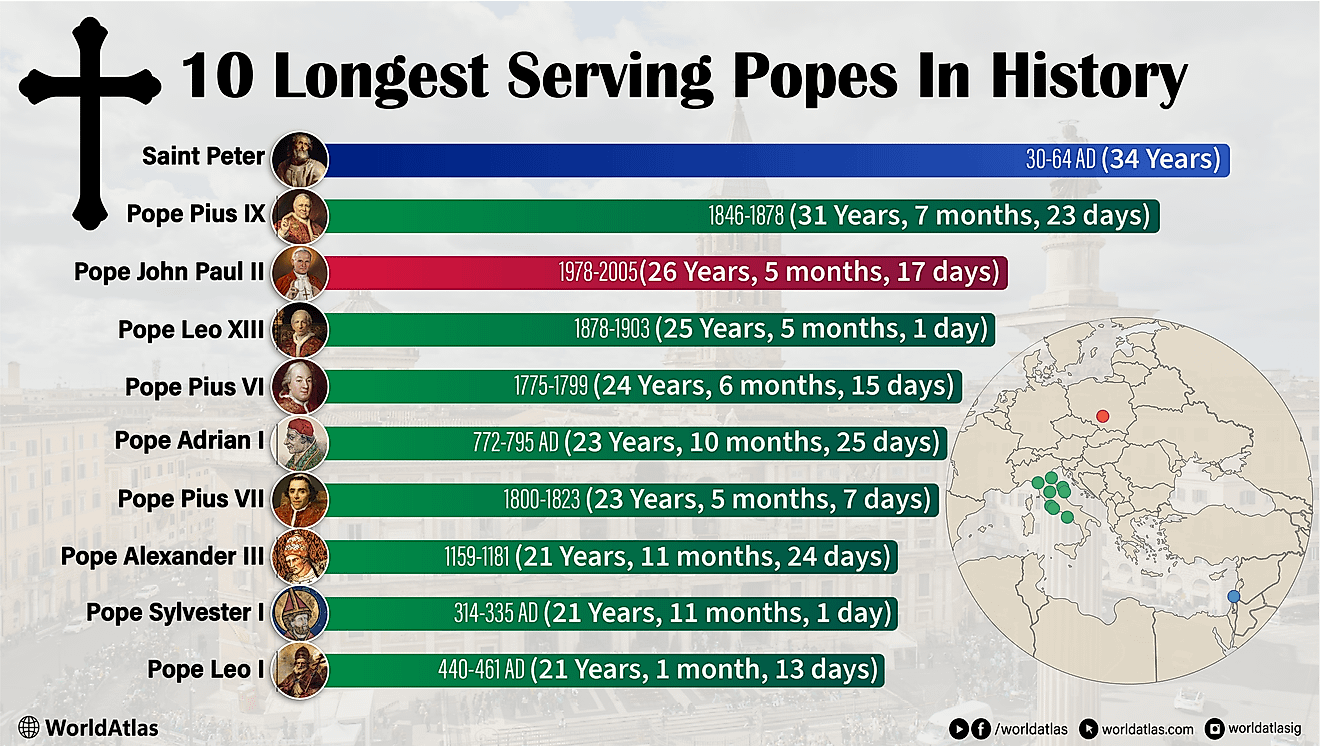
What Are the Different Types of Map Projections?
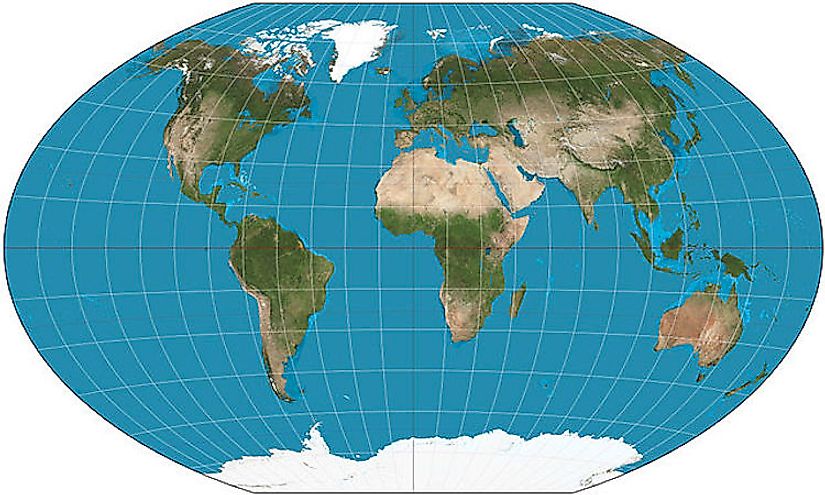
Map projections are a systematic transformation of longitudes and latitudes of a location on the surface of the sphere. Map projections are important in creating maps with map projections distorting the surface in some way. Some of the distortions on the maps are acceptable while other distortions are not acceptable depending on the purpose of the map. The map projection is classified depending on the type of projection surface on which the globe is projected conceptually. There are several map projections which preserve some of the properties of the sphere at the expense of others.
Types of Map Projections
Cylindrical
A cylindrical projection is any projection in which the meridians are mapped to parallel spaced vertical lines and latitudes are mapped to horizontal lines. The projections stretch from east to west according to their geometric constructions and are the same at any chosen latitude. Cylindrical projections are distinguished from each other by the north to south stretching denoted by φ. The north to south stretching equals east to west but grows with latitude faster than east to west stretching in the case of central cylindrical projection. Mercator projection is an example of cylindrical projection which became a standard map projection because of its ability to represent lines of steady course. Mercator distorts the size of geographical objects because its linear scale increases with the increase in latitude. The distortion caused by the Mercator distorts the perception of the entire planet by exaggerating the areas laying far from the equator.
Pseudocylindrical
Pseudocylindrical projections present the meridian as a straight line while other parallels as sinusoidal curves which are longer than the central meridian. The scaling of the pseudocylindrical projections are straight along the central meridian and also along the parallels. On a pseudocylindrical map, points further from the equator have higher latitudes than other points, preserving the north-south relationship. Pseudocylindrical projections include sinusoidal with same horizontal and vertical scales. The Robinson projection was created to show the globe as a flat image readily. The projection is neither equal-area nor conformal because of the compromise to show the whole planet. The meridians of the Robinson projection curves are gently stretching the poles into long lines.
Van der Grinten Projection
Van der Grinten is a compromised projection which is neither equal-area nor conformal. It is an arbitrary scaled projection of the plane projecting the entire earth into a circle. Van der Grinten projection preserves the image of Mercator projection and reduces its distortion. However, the Polar Regions can still be distorted by the Van der Grinten projection.
Conic Projection
Conic projections have meridians mapped to equally spaced parallels originating from the top while the parallels are mapped to circular arcs which are centered at the top. Two standard lines visualized as secant lines are picked in the process of making a conic projection. When a single parallel line has used the distance along the parallels is stretched. Examples of conic maps include equidistant, Albers, and Lambert conformal conic.
Pseudoconic Projection
Pseudoconic Projections are projections with parallels which are circular arcs with common central points. Unlike conic projections, the meridian is not constrained to be a straight line. Examples of pseudoconic projections include "bonne", which is an equal-area map projection. The maps are not constrained to rectangles or discs. Pseudoconic projection is one of the oldest map types and although they were used by Ptolemy, they are seldom seen today.
Scale Distortions On Map Projections
Map projections without distortions would represent the correct distance, direction, shapes, and areas on a map. However, map projections have distortions which depend largely on the size of the area being mapped. Scale distortions on maps are shown on the map by an ellipse of distortion or using scale factor which is the ratio of the scale at a given point to the true scale. Distortions on maps of countries or cities are not evident to the eye and can only be identified when computing distances and areas.
What Are the Different Types of Map Projections?
| Rank | Map Projection Name | Examples |
|---|---|---|
| 1 | Cylindrical | Mercator, Cassini, Equirectangular |
| 2 | Pseudocylindrical | Mollweide, Sinusoidal, Robinson |
| 3 | Conic | Lambert conformal conic, Albers conic |
| 4 | Pseudoconical | Bonne, Bottomley, Werner, American polyconic |
| 5 | Azimuthal | Gnomonic, Lambert azimuthal equal-area, Stereographic |
| 6 | Polyhedral | Authagraph, Octant projection, Cahill's Butterfly Map |
| 7 | Other | GS50, Peirce quincuncial, Van der Grinten |