What is Longitude?
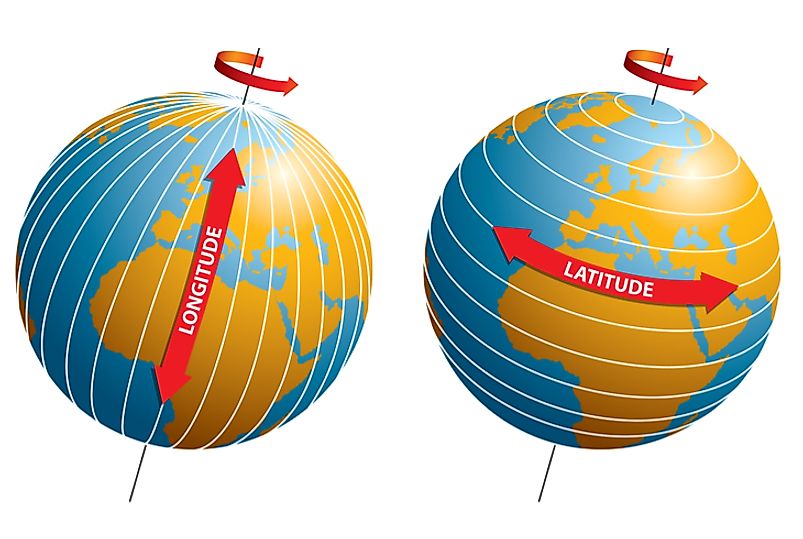
Longitudes are geographical points of direction that identify how east or west a position is on the Earth. The points are measured in degrees and symbolized by the Greek letter λ (Spelt as lambda). Also, there are special lines that run through the North Pole to the South Pole connecting points on the same longitudes. These lines are called meridians. The most special meridian is referred to as the Prime Meridian. This particular longitude runs through Greenwich in England. It holds the position of zero degrees (0°) longitude. In order to establish the longitude of other places on Earth, the places are measured by the angle east or west in relation to the prime meridian. It starts from 0° on the east side to +180 and to the west, side the angle goes up to -180. A place's location north or south of the Prime Meridian is measured by latitude. This can be described as the angle between the local longitude and the equator.
It is important to note that the Earth is not a perfect sphere. If it were a perfect sphere then the longitude at a particular place would be equal to the angle between vertical north–south plane through that place and the plane of the Prime/Greenwich Meridian. It is a good thing that the Earth is not uniform, the presence of mountains and other irregularities on Earth’s surface make it possible to shift the vertical plane a distance from the axis. When an intersection between a north to south plane and the Greenwich/prime meridian happens, an angle is created and this angle forms the accurate astronomical longitude. The longitudes that are identified by maps are formed by the angle between the meridian that passes through Greenwich and a plane that passes perpendicularly through the curvature chosen as Earth’s sea level. This measurement is not very accurate since the Greenwich plane does not go through the actual sea level.
Origin and Discovery
The history of the longitude has been contributed upon by great minds in the fields of astronomy, map making, and navigation over many centuries. This information was and still is important. For example, in safe ocean plotting, a means of defining the longitude and latitude was very much needed. The process of finding precise measures took centuries and the contribution of very great scholars. The earliest works recorded on research on the longitude was in the 3rd century BCE by Erastosthenes. His work was later build up by one Hipparchus in the 2nd century BCE. The 11th century revealed a great mind by the name Al-Burini who discovered that the earth rotated on its axis, a discovery that forms the basis for the modern belief of how longitude and latitude are related.
Initial Solutions
In the pursuit of greatness, nations had to invest in overseas trade, settlements, and outposts. For this reason, the need for identifying the location of their ships in the sea using its longitude was of high importance. Nations like France, Spain, and the Netherlands offered great prizes towards the solution of the longitude issue.
One of the earliest solution to the longitude problem was based on time gaps. The method involved sailors determining the local time by using the sun as a reference point in comparison with their local time. This method solved the challenge of mechanical clocks not working at sea due to humidity and the motions at sea.
Britain's Charles II started the Royal Observatory in 1675 so as to find out the longitude of places in order to aid navigators. A method called The Lunar Distance Method was discovered, where an accurate location of stars was recorded, then the moon’s motion in relation to the stars could be used to calculate the time at Greenwich. The challenge in this method was predicting the moon’s motions and lack of availability of accurate instruments for the observation.
The 1714 Longitude Act
The year of 1714 was a great year for the longitude research. The British government offered a prize of £20,000 for a solution to the longitude question by a closeness of half degree, which is an equivalent of 2 minutes. As a motivation, two solutions were created at the same time. A clock maker by the name John Harrison made the first relevant contribution through his creation of the Marine Timekeeper H4. This instrument was later renamed the Marine Chronometer. The other contributors include John Hadley, and the German astronomer Tobias Mayer, who perfected the earlier astronomical catalogues and instruments to be used in the Lunar Distance method. The Astronomer Royal Nevil Maskelyne made notable contributions through his efforts on the Nautica Almanac and the Board of Longitude. The Royal Observatory remains a testing point for marine scholars and astronomical observers. These efforts contributed highly to Greenwich becoming the referential Prime Meridian.
Longitude Calculations
Longitude is denoted by an angular measurement starting at 0° to +180° eastwards and -180° westwards. Lambda (λ) has been used to denote places location east or west of the Prime Meridian. Each degree of longitude apart is separated by 60 minutes and a minute is in turn divided into 60 seconds. For accuracy purposes, the seconds are captured by decimal points as such 23° 27.5′ E. This position can also be written as a decimal fraction as such 23.45833° E. The angular part can also be conveyed as radians to be used in calculations as a signed fraction of π (pi), or an unsigned fraction of 2π. During calculations, the west/east suffix is dropped to be replaced by the negative symbol (-) west of the Prime Meridian while the positive sign (+) is used to denote places east of the Prime Meridian. An intersection of a specific longitude and a specific latitude is then used to calculate the position of a place on Earth.
To determine the longitude of a place, the time difference between that place and the Universal Coordinated Time (UTC) is calculated. Speed of sun movement across the sky = the number of degrees in a circle/number of hours in a day = 360° ÷ 24 hours = 15° per hour. Therefore, for a person 4 hours ahead of UTC, that person is near 60° longitude (4 hours × 15° per hour = 60°). In order to be accurate on this calculation, one needs to have a chronometer fixed at UTC and also be able to determine a place’s local time using astronomical observation or solar means.
Singularity and Discontinuity of Longitude
In mathematics singularity can be defined as a point at which a mathematical entity cannot be defined or it fails to behave in a particular normalized way of such entities, while discontinuity is defined as the lack of continuation of a function at a point in its field. While doing calculations it is important to know that the longitude is singular at the poles so calculations may not be very accurate at such points. The point ±180° Meridian represents a form of discontinuity that must be carefully handled. To predict and avoid errors in calculations, the longitude and latitude could be replaced by the horizontal position representation during calculations.
Influence of Tectonic Plates on Latitude
The tectonic plates are constantly moving at a speed of 50-100mm per year. This means that different places on Earth are always moving in relation to one another. This movements increase the longitudinal distances between two points at any particular place. For example, the difference between Uganda on the African Plate and Ecuador on the South American Plate is increasing by around 0.0014 arc seconds per year. To reduce the change in longitude or latitude between place on the same plate a reference frame can be used where the points/coordinates are fixed on a singular plate like NAD83 for North America.
Length of a Degree of Longitude
The length in miles or any other measurement of a degree between longitudes is solely dependent on the radius of the latitude circle. Since the degrees of latitudes are parallel, you will find that the distance between each degree of latitudes will remain almost constant. On the other hand, since the degrees of longitudes are wider apart closer to the equator and closer at the poles, the distance between two longitudinal points vary greatly. The approximate degree of latitudes is 69 miles apart, but this figure varies on a range from 68.703 miles near the equator to around 69.407 near the poles. A degree of the longitude has been recorded to be the highest at the equator at 69.172 miles at the equator. This figure gradually reduces to 0 at the poles as the longitudes merge into one.