What Is The Earth's Energy Budget?

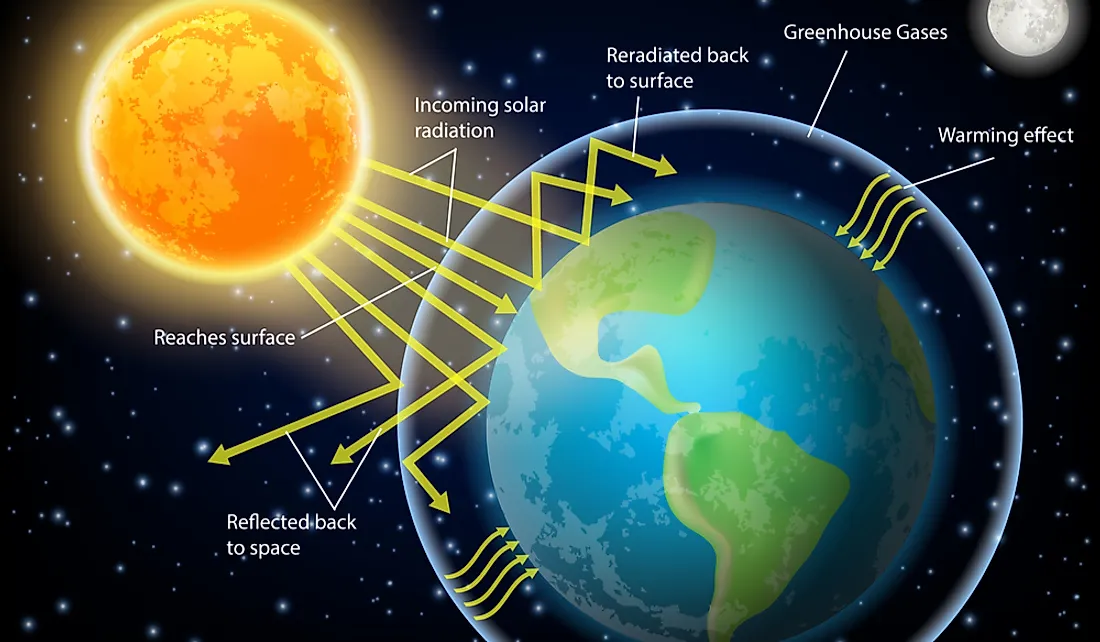
The term ‘earth's energy budget’ was coined to refer to the energy the planet receives from the sun, utilized all over the earth, and then sends back into space. The sun provides all the energy that is utilized within the earth although most of the sun's energy never reaches the planet's surface. The heat that the earth receives goes into five distinct components of the environment: living things such as plants and animals, the earth's crust, the earth's water bodies, the atmosphere, and the ice. Due to the shape of the planet, the amount of energy that strikes the earth's surface is significantly uneven with some areas receiving substantially greater amounts of heat than others. The earth's shape also makes it so that the polar areas receive considerably less heat than the regions closer to the equator. Scientific research has shown that each square meter on the earth's surface receives and gives back approximately 240 watts of energy from the sun. The amount of heat energy received by the earth and radiated back to space is close to being balanced with the earth nearly approaching a state of radiative equilibrium.

Incoming Heat Energy

The earth receives solar energy in the form of shortwave radiation. The incoming energy may interact with the earth's environment in three different ways: scattering, absorption, and reflection. If the solar radiation strikes the earth's surface without undergoing any of these three processes, it is referred to as direct solar radiation.

Scattering

When the sun's energy is scattered, it comes into contact with minute particles such as gas molecules which then change the direction of the sun's rays without altering the wavelength. Scattering is dependent on many factors such as the radiation's wavelength as well as the size of the molecules scattering the radiation. The main effect of scattering is that it reduces the amount of heat energy reaching the earth's surface. Scattering is also responsible for the earth's sky being blue. Scattered solar radiation that strikes the earth's surface is referred to as diffused solar radiation.

Absorption

Another way through which solar energy interacts with the earth's environment is by absorption. Scientists describe absorption as the process through which a substance takes in solar radiation then changes into heat energy. After the material generates heat energy, it later radiates it back to the environment through longwave radiation.

Reflection

Solar radiation may also be reflected when it interacts with particles within the earth. Reflection occurs when sunlight strikes a particle and is redirected into the atmosphere. The main impact of reflection is that it reduces the amount of heat reaching the earth's surface. Reflection typically occurs within the clouds where water droplets intercept and redirect the sun's rays.

Outgoing Heat Energy

The earth sends out energy into space in the form of longwave radiation which usually has low quantities of energy. The energy sent from the earth is generally in the form of infrared radiation. Particles within the environment absorb some of the energy radiated from the earth while clouds also reflect some. Outgoing radiation is fundamental to the earth's energy budget as it is the sum of the energy from the earth to the atmosphere. Outgoing radiation also plays a significant role in the greenhouse effect as gases such as carbon dioxide and methane absorb the radiation increasing the quantity of heat within the atmosphere. Another effect of the absorption by these gases is that it results in the temperature of the earth's surface increasing. Scientists indicate that a higher concentration of greenhouse gases may lead to global warming.

Energy Imbalance within the Earth

In case the energy coming into the earth and the energy that leaves the planet are not equal, the earth gains or loses energy. There are two primary ways to check whether the earth is gaining energy, losing it, or is in balance. One way is through the use of indirect measurement. In case of an energy change on the earth, it will affect various components of the earth's environment such as the oceans. To measure the change, using the ocean devices known as argo floats are utilized. Another method that can be used is through direct measurement primarily through the use of satellites. The satellites that measure the energy imbalance use technology developed by NASA and they monitor the amount of heat that the earth receives as well as the amount that the earth radiates.

Greenhouse Effect

The gases that make up the most significant percentage of the earth's atmosphere are oxygen and nitrogen which interact with neither incoming solar radiation nor thermal radiation from earth into space. The earth's atmosphere, however, also contains substances such as water vapor and other gases that absorb thermal radiation of specific wavelengths. Five to six percent of the energy that the earth radiates is absorbed by the substances and the increase in their concentration in the atmosphere results in a higher rate of absorption. The primary impact of the standard greenhouse effect is that it raises the earth's temperature making the earth warmer than it would be if it relied purely on the sun for heating.

Climate Change

The climate of the earth may change due to natural factors or due to the influence of humans. Natural factors that result in the alteration of the earth's climate include volcanic eruptions and the alterations in the brightness of the sun which would either increase or reduce the amount of solar energy reaching the earth's surface. A number of human activities contribute either directly or indirectly to altering the earth's climate such as releasing pollutants into the atmosphere as well as deforestation. The climatic changes have a direct impact on the earth's energy budget.

Economic Impacts of Climate Change

One of the sectors substantially affected by changes in the earth's climatic patterns is the agricultural sector. Due to the changes, some regions are experiencing less rain than they would typically which leads to crop failure. Other areas are experiencing higher than average rainfall leading to the destruction of crops in the farms. The impact of these events is that it reduces the crop yields making it more difficult for farmers to make a living and creating food shortage. Another effect of climate change is that it will lead to a significant increase in cases of heat waves some of which may cause death reducing the section of the population able to contribute to the economy.